NeoLoad – Correlation (Handling Dynamic Value)

Once you record the navigation flow of AUT (application under test) and check the user path the next step is handling the dynamic value that is ‘Correlation’ in the NeoLoad script. As I explained in the correlation topic of LoadRunner and JMeter, there are 3 steps involved in the correlation which are:

1. Identification of Dynamic Value
2. Implementation of Correlation Logic
3. Replace the Dynamic Values with the Correlation Variable

These three steps are also applicable for NeoLoad. So, let’s understand step-by-step the correlation in NeoLoad.

Identification of Dynamic Value

The first step is the identification of the correct value which is coming from the server and that value gets changed with respect to the user or request or time. Since NeoLoad has the option to identify the dynamic values automatically based on the custom pre-defined rule (Framework Parameter) or generic rule. You can use the automatic correlation option that helps to identify and correlate the dynamic values by scanning the recorded script (Refer to Script Recording article). You can also skip this option if you are confident enough to carry out the manual correlation.

In some complex cases, NeoLoad is unable to identify all the dynamic values, hence you have to go for manual correlation.

The easiest way to start the dynamic value identification method is ‘Check User Path’. Run the ‘Check User Path’ and validate the script against ‘New User’. If it fails then there is a possibility of correlation in that particular request. Let’s see with an example:

In the above example, favicon.ico is failed while performing user path validation and threw an HTTP 404 error which indicates a client-side error. Hence your investigation starts from this point. Anyway, this is just an example.

Let’s consider, that we have identified a value ‘BIRDS’ as a dynamic value that we need to correlate. Now, move to the correlation logic implementation part.

Implementation of Correlation Logic

After the identification of the dynamic value, the next step is to implement the correlation logic. Follow the below steps once you find out the correct dynamic value. Please note in this case, we have to correlate ‘BIRDS’.

1. Go to the step that has dynamic value. ‘BIRDS’ is passing in the third request and it is the value of the ‘categoryId’ parameter.

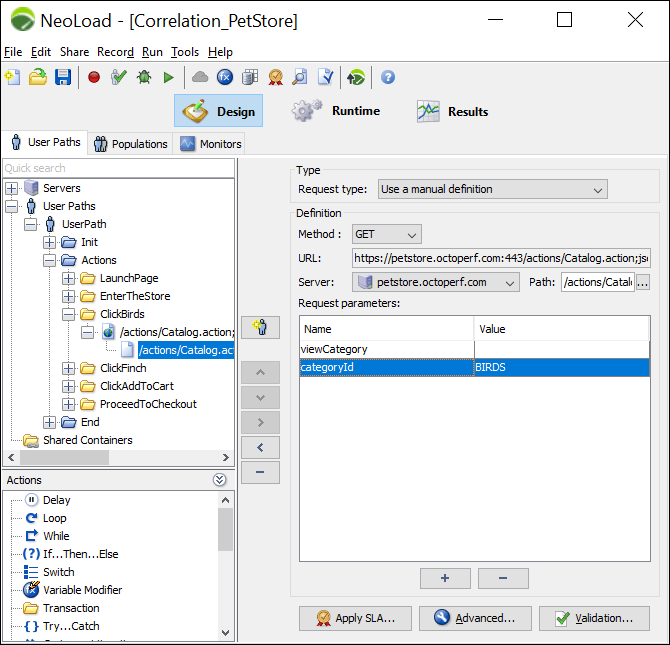
2. Right-click on the dynamic value and select ‘Flag in the responses’.

3. NeoLoad will highlight the request(s) and transaction(s) containing the dynamic value in the response. You can see a checkmark over the icon of Action, Transactions and Requests.

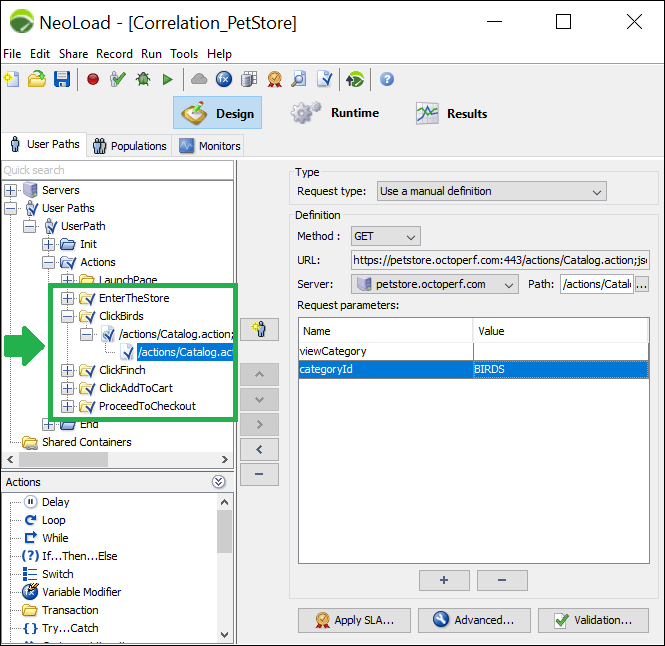
4. Click on the very first transaction with a check mark.

5. Select the very first request, under that transaction. This is the request whose response contains the required dynamic value.
6. Then, click on the ‘Advanced’ button given at the bottom of the pane.

7. ‘Advanced’ pop-up appears.

8. Go to the ‘Recorded response’ tab

9. Press ‘Ctrl + F’ to search the dynamic value. You can see a search bar appear at the bottom with ‘Find’, ‘next’, ‘previous’, ‘Match case’ and ‘Highlight’ options.

10. Type the text or dynamic value, and NeoLoad will find and highlight the value in the blue background. You can search for more occurrences of the value by pressing the ‘next’ button. Use the ‘Match case’ and ‘Highlight’ options as per your convenience.

11. Select the left and right boundary text along with the dynamic value so that you can implement the search logic. The selected string must be unique so that dynamic value can be identified easily. Refer to the below screenshot in which the selected string is viewCategoty=&categoryId=BIRDS”. Here, ‘viewCategoty=&categoryId=’ will be considered as a Left Boundary and ” (double quote) will be considered as a Right Boundary.
12. Copy the selected string.

13. Go to ‘Variable extractors’ tab
14. Click ‘+’ (plus sign) available at the bottom

15. ‘Variable Extractor’ pop-up appears with the ‘Definition’ tab.

16. Now, provide the below information in the respective fields:
    1. Variable name: The name of the correlation variable which will be used in the script. This variable will replace the dynamic value that appears in the subsequent requests in the script
    2. Extract the value from: It defines the search criteria where dynamic value will be available. The search criteria are:
       1. Body
       2. Header
       3. Both
       4. Variable
    3. Expression: For a JSON or XML format response, enable this option and provide the respective value.
    4. Look in the response body for sentence:
       1. Starting with: Paste the copied text of ‘Left Bounday’ in step 11.
       2. Followed by: Define the format of the dynamic value whether it is number, text, alphanumeric etc. This field helps to identify the correct dynamic value.
       3. Ending with: Paste the copied text of ‘Right Boundary’ in step 11.
    5. Occurrence to extract: It specifies the occurrence or place of the value. As you can see 5 is given in the screenshot which means the required value is available at 5th place. Now here the question is how to get the place number of the dynamic value. So to answer this, you also need to look into the value that appears in the field ‘Value extracted from recorded content’. It is fine if the shown value is as same as the dynamic value; otherwise, increase the value by one and verify the text. The default value is 1.
       In this example, providing 5 in the field gives BIRDS in the field of ‘Value extracted from recorded content’. Hence 5 is the correct place number that matches with the required dynamic value.
       Some other options are also available like:
       1. Extract all occurrences: To extract all the values that satisfy the search condition.
       2. Random extract one occurrence: To extract a random value from a list of identified values
    6. Value is encoded as: This option is helpful for encoded value. Select the appropriate option from the dropdown list as per your requirement.
    7. Value extracted from recorded content: It shows the searched text in the response as per the input provided in the ‘Occurrence to extract’ field.

17. Click ‘OK’
18. You can see a new row gets added under the ‘Variable extractors’ tab along with the regular expression.

Replace the Dynamic Values with correlation variable

Once the steps of identification of dynamic value and implementation of the correlation logic are completed then replace all the occurrences of dynamic value with the correlation variable in the test script. Follow the below steps:

1. Select the row of respective variable and click ‘Search and replace’ button.

2. ‘Search and Replace’ pop-up appears
3. Click either the ‘Replace all’ or ‘Replace manually’ option. Let’s select ‘Replace manually’ so that you can understand which values are getting replaced in the script.

4. NeoLoad displays the requests one by one which contains the dynamic value and provides ‘Previous’, ‘Current’, ‘Next’, ‘Replace’ and ‘Replace All’ options in the ‘Search/Replace’ pop-up. Use the given options as per your need and replace the dynamic values.
5. Click the ‘Replace’ button

6. The value will be replaced by the defined correlation variable and will look like this. Refer to the below screenshot.

If there are more than one dynamic values then apply the same steps for all the dynamic values and correlate them.

---

You may be interested:

• NeoLoad Tutorial

---