Written By: Swetha Pujari
Due to the company’s network/firewall policy, sometimes setting up the connectivity between master and slaves in JMeter’s Distributed Testing has obstacles or delays due to firewall requests. As an interim solution, we can use Parallel Testing to execute higher loads by dividing the load across multiple machines. This is a good alternative to JMeter Distributed Testing.
What is Parallel Testing?
This type of testing approach involves running the test scenario across multiple machines simultaneously, thereby aggregating the preferred total number of users against the application under test (AUT). For instance, if the requirement is to test for 1000 users, we configure the test run in two different machines with 500 users each at the same time.
Under Distributed architecture, all machines are synchronized and in constant communication. Master commands the slave machines on when to start and stop the test, and Slave machines, in turn, send test results to the Master machine in near real-time.
For Parallel Testing, the two or many testing systems used are independent entities and focus on injecting load against the AUT.
Note: Remember to input separate CSV/test data files for the test script/s in different machines unless the data needs are not unique such as search keywords or drop-down values. If the data used is login/password, then each test system needs to have its separate data files to facilitate unique user
Where is the problem?
Parallel testing’s dilemma lies in collating the results when there are two or more JTL files/ test logs from the multiple test executions rendered against the AUT. Merge Results comes to the rescue to fix this predicament.
‘Merge Results’ is an element to merge multiple files of JMeter test results
With parallel testing, you install JMeter on multiple machines and trigger the tests against the AUT (application under test) at the same time. Once the tests are complete, with the help of the ‘Merge Results’ plugin, you can merge multiple results files together into a single .jtl file, thereby generating a single Load test report.
Jar to download: jmeter-plugins-mergeresults-2.1.jar.
Source: https://jmeter-plugins.org/wiki/MergeResults/
Download the above plugin from the Plugin Manager and place it in the ‘ext’ folder of JMeter.
apache-jmeter-<version> -> lib -> ext

Now, restart the JMeter instance before use.
Follow the below steps in order to merge two JTL files and generate a single JTL
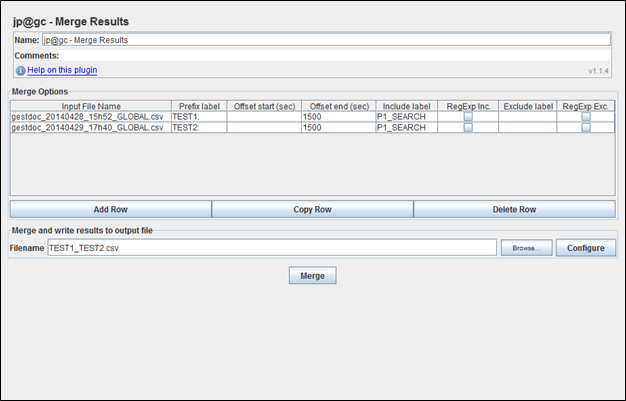
Once the Merge results tab opens, browse the JTL files and insert the path to the Output file before clicking the Merge button. If the output file already exists, it will be over-written.
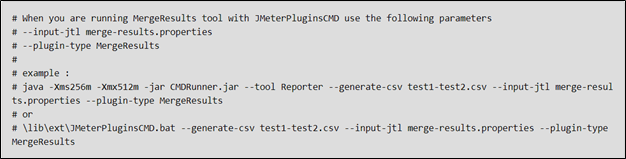
The same can be accomplished from the Command line as follows:
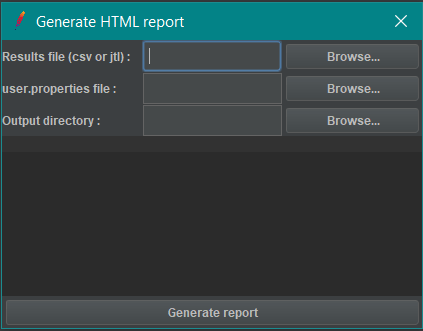
HTML Report Generation
After generating the consolidated file with .jtl extension, creating an HTML report should be easy by following the Generate HTML Report tool in JMeter.
- Results file (csv or jtl): Browse the generated .jtl file
- user.properties file: Browse the user.properties (in jmeter/bin folder) of the JMeter instance which was used during the test.
- Output directory: Browse the empty folder path where you want to save the HTML report.
IMPORTANT NOTE:
As this strategy might skew the results, it is advisable to use it for a loose representation of test results and only utilize it in contrast to the JMeter-approved distributed testing approach.
You may be interested:

